Cavendish, uno de los científicos más importantes del siglo XVIII, pasó a formar parte de la Royal Society en 1760. Es una sociedad científica fundada en el año 1660 en Reino Unido cuyo objetivo principal es promocionar el Saber Experimental Físico-Matemático. Esta organización no obtuvo logros como tal, fueron los participantes de ésta los que consiguieron grandes avances, entre ellos: Darwin, Robert Hooke, Benjamin Franklin, Newton (que llegó a ser presidente), Stephen Hawking, Richard Dawkins...
Cavendish, como los anteriores científicos también realizó diferentes descubrimientos, como la composición química del aire y estos fueron sus resultados:
Hemos realizado un diagrama de sectores en el que podemos observar mejor la proporción de los componentes del aire.
Los dos componentes principales son el nitrógeno y el oxígeno, y el resto de componentes a penas se pueden apreciar. Cavendish demostró esto mismo casi de forma exacta y con unos resultados prácticamente perfectos.
El flogisto se suponía que era una sustancia invisible que existía en todas las cosas materiales y que explicaba su combustión. La teoría del flogisto trataba de explicar porque algunos elementos era combustibles y otros inflamables. Georg Ernst Stahl, su creador, pensaba que todos los elementos combustibles estaban formados en parte por flogisto. Pero fue Lavoisier quién más tarde demostró que esta teoría era falsa probando que se trataba de reacciones químicas.
Cavendish también descubrió cuales eran las propiedades del hidrógeno, un elemento químico perteneciente al grupo de los no metales. Es el primer elemento de la tabla periódica y un gas inodoro, incoloro e insípido. Tiene un único protón y un solo electrón, y una densidad de 0,071 g/L. El hidrógeno es uno de los componentes del agua, H2O, que está formada por dos átomos de hidrógeno y uno de oxígeno. El agua es fundamental para la vida , ya que todos los seres vivos estamos formados en gran parte de ella.
Algunos de sus estudios estuvieron basados en el calor específico de las sustancias. El calor específico es la cantidad de calor que necesita un cuerpo por kilogramo para que su temperatura se eleve 1 grado centígrado. Es una magnitud física que indica la capacidad de una materia para almacenar energía interna en forma de calor.
La ley de Coulomb se puede expresar como la magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario.
La diferencia que encuentro con la ley de gravitación universal es que en esta última, las masas siempre son positivas, mientras que la ley de Coulomb solo atrae entre cargar de signos opuestos.
Un condensador eléctrico es un dispositivo pasivo, utilizado en electricidad y electrónica, capaz de almacenar energía sustentando un campo eléctrico. Está formado por un par de superficies conductoras, generalmente en forma de láminas o placas, en situación de influencia total separadas por un material dieléctrico o por el vacío. Las placas, sometidas a una diferencia de potencial, adquieren una determinada carga eléctrica, positiva en una de ellas y negativa en la otra, siendo nula la variación de carga total.
Para construir un condensador eléctrico casero necesitaría un recipiente no metálico con agua salada tibia. Luego habría que envolver la parte exterior del recipiente con papel de aluminio y Colocar un objeto de metal (como un cuchillo, un clavo, etc.) en el agua salada sin que este objeto de metal toque el papel aluminio. Esta lámina es un terminal, y el objeto metálico es el otro. Y por último habría que Cargarlo conectando las dos terminales a una corriente eléctrica como por ejemplo una batería normal del hogar
Y por último, si usamos por ejemplo el hierro o el acero para realizar el experimento interferiría con el campo magnético, y hay que intentar evitar esto. El magnetismo o energía magnética es un fenómeno físico por el cual los objetos ejercen fuerzas de atracción o repulsión sobre otros materiales. Hay algunos materiales conocidos que han presentado propiedades magnéticas detectables fácilmente como el níquel, hierro, cobalto y sus aleaciones que comúnmente se llaman imanes. Sin embargo todos los materiales son influidos, de mayor o menor forma, por la presencia de un campo magnético.
El magnetismo también tiene otras manifestaciones en física, particularmente como uno de los 2 componentes de la radiación.
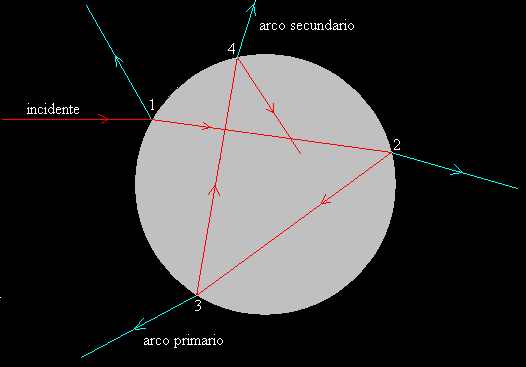
La reflexión de la luz es el fenómeno de cambio en la trayectoria de propagación de la luz. En la reflexión de la luz el ángulo de incidencia es igual al ángulo de reflexión y el rayo incidente, el reflejado y la normal se encuentran en un mismo plano.
